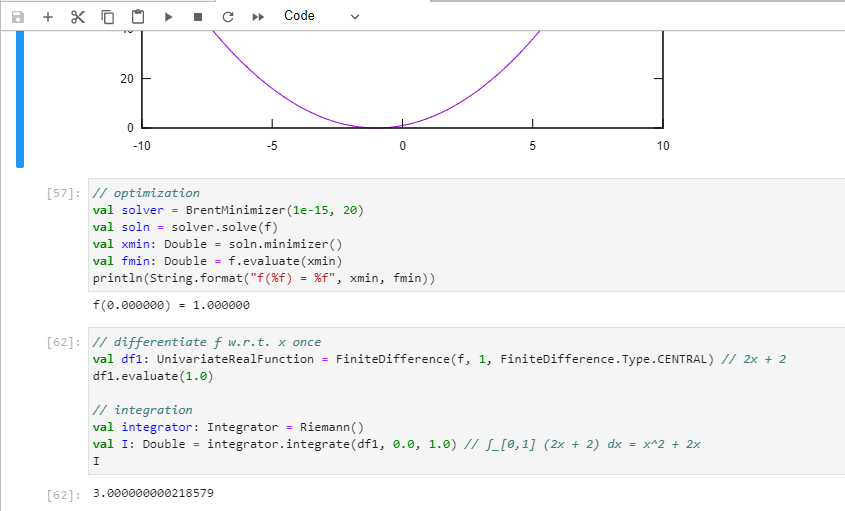
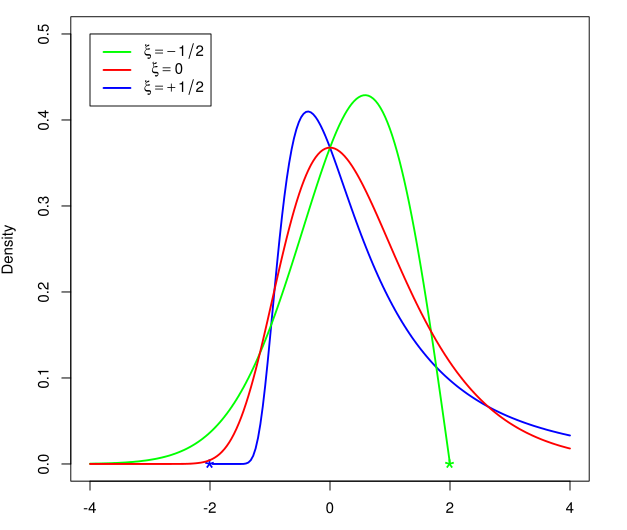
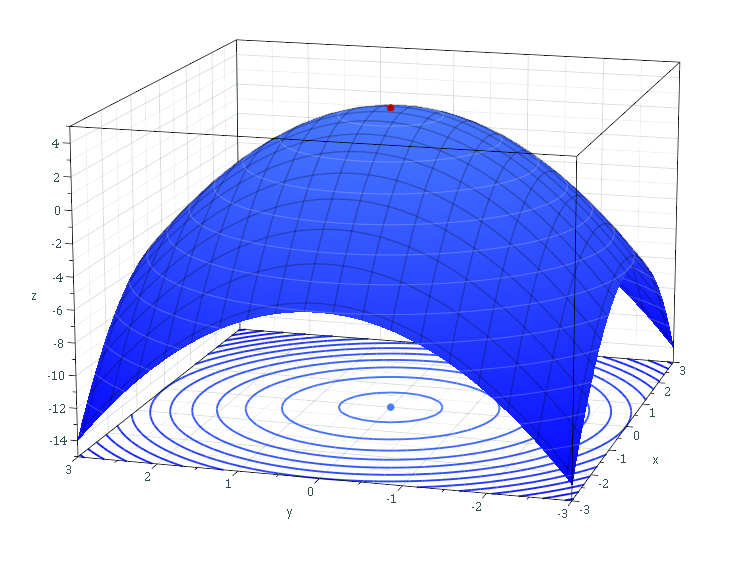
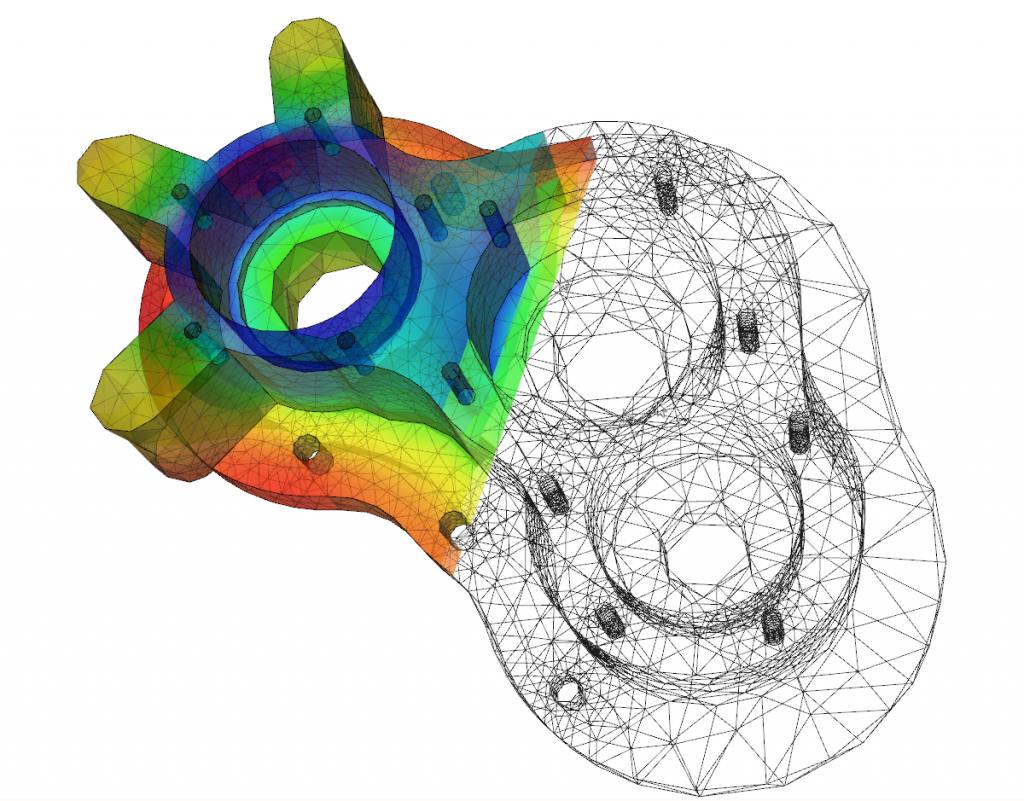
NM Dev is an object-oriented, high performance, extensively tested, and professionally documented programming library of mathematics that runs on S2. Having been developed since 2010, it is a large collection of numerical algorithms so coded such that they are solidly object-oriented, unified and testable. A user, who has little programming experience or mathematical sophistication, can easily create a solution for his or her complex engineering problem by quickly putting together classes.

    SuanShu, now an open source project, has been replaced with NM Dev which has improved capability. NM Dev is also commercially supported. See our setup guide to get started using NM Dev on your local machine, or try it with our very own S2 IDE.

    We have recently published a book that teaches math or numerical programming in Java using NM Dev/SuanShu. There are plenty of examples, which can be found in GitHub.

    S2, an Integrated Development Environment (IDE) for data science. Built using Java technology and NM Dev, it enables data scientists to write high performance code that runs on devices with a JVM. Compared to Python, it is much faster and is much easier to deploy. S2 is a one-stop shop of advanced analytics and data for engineers to quickly prototype computation models. See our available libraries here.

    Click to try now. Happy coding!

    S2 IDE

    Features

    Linear Algebra
    Statistics
    Digital Signal Processing
    Calculus
    Time Series Analysis
    Extreme Value Theory
    Optimization
    Differential Equation

    Benchmarks

    NM Dev is probably the fastest linear algebra library in Java!

    NM Dev has a suite of high performance optimization algorithms.

    We offer a limited trial for NM Dev, the Java numerical library.

    Download here:

      nmdev-1.2.4.zip (13.8 MiB, 3,811 hits)

    We can further improve NM Dev to suit your needs by adding functions, improving speed and optimize it as per your requirements as a consulting project.

    NM Dev distribution is deployed in NM’s repository. To let maven be aware of this repository, add the following repository definition to the pom.xml in the <repositories> section:

    <repository>
    <id>nm-repo</id>
    <name>NM maven repository</name>
    <url>https://repo.nm.dev/repository/maven-public/</url>
    <layout>default</layout>
</repository>

    To use NM Dev, in the <dependencies> section, add:

    <dependency>
    <groupId>dev.nm</groupId>
    <artifactId>nmdev</artifactId>
    <version>1.2.4</version>
</dependency>

    Licensing

    License Agreement

    Community License

    • BASIC
    • OPTIM
    • STATS
    FREE!
    We have released a previous version of the source code in GitHub.

    Academic License

    • BASIC
    • OPTIM
    • STATS
    I am a student!
    If you meet our criteria for “Qualified Academic Users”, you may purchase an academic license. An “Academic License” allows you to use these 3 packages: BASIC, OPTIM and STATS.

    Commercial License

    • BASIC
    • OPTIM
    • STATS
    • O/PDE
    • EVT
    I am a professional!
    A commercial license lets you run selected modules on a machine permanently.
    Popular

    Contributor License

    • Customized
    Submit a proposal!
    If you contribute code to NM Dev and if your code is accepted by us, you may get a permanent license to use NM Dev.

    Our Customers

    This is a FREE, experimental version of the SuanShu library for the dot net environment. To download, register with us and login.

      suanshu.net-3.0.1.zip (13.1 MiB, 872 hits)
    You do not have permission to download this file.

    For more information, see: